In my not so humble opinion Quantum Circle Notation is the best way for a budding QC developer or scientist to get started in this field. Simultaneously I find it to be a great way for experienced individuals to effectively convey their ideas. This claim might be a bit bold considering that this notation has not been widely accepted by the community but I’m hoping to make a compelling argument in this post.

Where does it come from?

Circle Notation was invented by Eric Johnston and is used heavily in his book and on his online quantum simulator.

As such, we will be referencing both his book and his simulator extensively, thanks for your hardwork Eric!

The Elevator Pitch

Circle Notation is a way to represent the state of a quantum circuit visually. Referring back to the last post, a 2 qubit quantum state would look something like this mathematically: $|\psi\rangle = \alpha_{0}|0\rangle + \alpha_{1}|1\rangle + \alpha_{2}|2\rangle + \alpha_{3}|3\rangle$ where $|\alpha_0 + \alpha_1 + \alpha_2 + \alpha_3|^2 = 1$. This last part is the complex modulus squared.

Substituting in some real values we might get a state that looks like this:

\[ |\psi_A\rangle = \frac{1}{\sqrt{2}}|0\rangle + 0|1\rangle + 0|2\rangle + \frac{1}{\sqrt{2}}|3\rangle \]

\[ = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|3\rangle \]

Or like this:

\[ |\psi_B\rangle = 0|0\rangle + \frac{1}{\sqrt{2}}|1\rangle + \frac{1}{\sqrt{2}}|2\rangle + 0|3\rangle \]

\[ = \frac{1}{\sqrt{2}}|1\rangle + \frac{1}{\sqrt{2}}|2\rangle \]

Just by looking at the equations its easy to see that $|\psi_A\rangle \neq |\psi_B\rangle$ but I find it difficult to really discern what the difference entails.

But by using Circle Notation down below we can easily visualize the difference between the states. Even though you may not yet be able to interpret all of the information packed into these images it is rather clear that there is a difference.

$\psi_A =$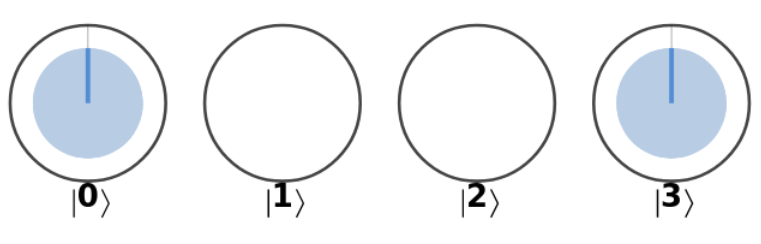

$\psi_B =$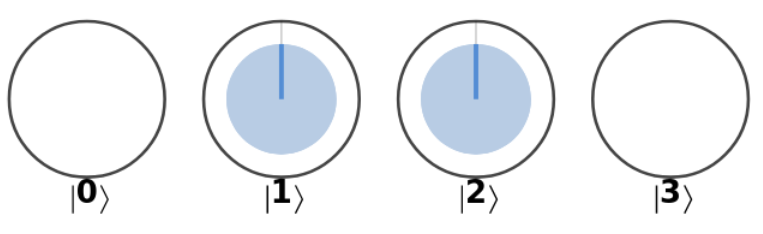

Deep(ish) Dive

Now that we know the notation can convey the same information as a complex equation lets dig into how we get the notation from the equation.

Each circle represents a state that can be represented by the qubit string. For $\psi_A$ there are 4 states in the state space and thus there are 4 circles. When we represent a quantum state in circle notation we always represent the whole state space.

Each state $s$ is represented by a drawing inside its corresponding state circle. The drawing is a direct representation of the state’s amplitude $\alpha_s$ where $\alpha_s$ is any arbitray $\alpha$ in $|\psi\rangle = \alpha_{0}|0\rangle + … + \alpha_{n-1}|n-1\rangle$.

Each state circle is a unit circle with radius 1 and has an inner circle drawn in it. The radius of that circle is the magnitude of the state $s$ which can be found by taking the complex modulus of $\alpha_s$ which looks like so: $|\alpha_s|$.

Magnitude

Remember that the square of the magnitude of a state $s$, shown as $|\alpha_s|^2$, is equivalent to the probability that you will read the state $s$ when measuring the system. The equation for the area of a circle is $A_c = \pi r^2$. This means that for each state circle, the percentage of area filled in by the inner circle is equivalent to the chance that you read out that state when measuring.

Ex: In $\psi_A$ state $|0\rangle$ has an inner blue circle taking up 50% of the that states area. This means when we measure that quantum system, there is a 50% chance we read out the state $|0\rangle$.

Relative Phase

Besides the magnitude, there is also the relative phase for each state $s$. You can calculate the relative phase by finding the angle of $\alpha_s$ in polar coordinates. Each $\alpha_s$ is a complex number $c = a + bi$ and the angle can be found using the equation $\theta = \tan^{-1}(\frac{b}{a})$.

This relative phase for each state is represented by the relative angle differences between each state’s radius indicator compared to the $|0\rangle$ state’s radius indicator.

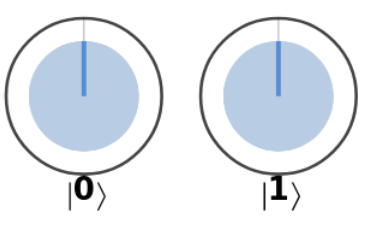
Looking at the states below ($|\psi_a\rangle$, $|\psi_b\rangle$, $|\psi_c\rangle$) notice that for $|\psi_a\rangle$ both radius indicators are inline. They are parallel to each other so their relative angle between each other, $\phi$, is $0^{\circ}$.

$|\psi_b\rangle$ radius indicators are pointing in opposite directions so $\phi$ is $180^{\circ}$.

$|\psi_c\rangle$ is the tricky one. The radius indicators look different from $|\psi_b\rangle$, but because $\phi$ is the relative angles between the radius indicators $|\psi_c\rangle$ and $|\psi_b\rangle$ are equivalent.

$$\|\psi_a\rangle$$	$$\|\psi_b\rangle$$	$$\|\psi_c\rangle$$

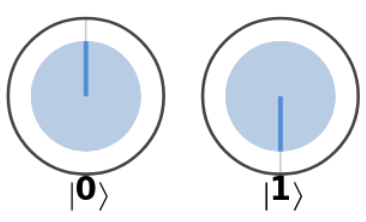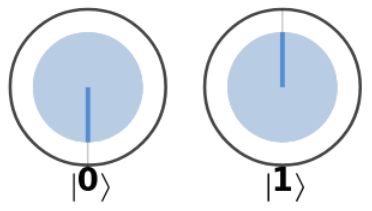Pros

Direct representation of the state vector
Easy to see which states are most likely to be measured
Relative Phase is easy to see
Entanglement is easy to see and accurately represented
Feels more similar to classical bit visualization and manipulation than other notations

Cons

Number of state circles scales with state space of the system
Not good at visualizing complex single qubit transformations through 3D space

For more information on Circle Notation checkout Programming Quantum Computers Chapter 2.

Circle Notation